※この講座は所属企業や所属団体とは一切関係ありません
決定木モデルとは

今回は、数式などは特に扱わず、ざっくりとどんなことをやっているのかを理解することを目的とする。例えば、あるお店の顧客データとして「優良顧客フラグ」「年齢」「メールマガジン購読フラグ」「前回来店日」「前々回来店日」のデータがあり、「優良顧客」を予測するモデルを決定木で構築することを考えると図表1のような結果が得られる。
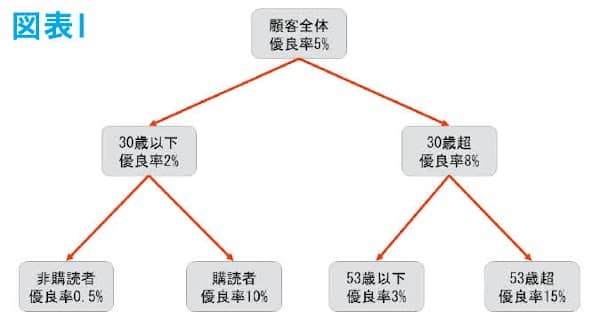
この図を説明すると、最初は顧客全体の集団で優良顧客の割合である優良率は5%となっているが、30歳以上かそうでないかの「条件」で左右に分岐され、左側の集団(30歳以下の集団)は優良率2%であり、右側の集団(30歳超の集団)は優良率5%となった。このように「条件」による分岐で優良率に差ができるようにどんどん分割していくモデルのことを決定木という。この例では、元々は全体で5%だったものが最終的には0.5%、10%、3%、15%と優良率の高い集団と低い集団に分けられている。優良顧客かどうか未知のデータ(顧客)に対して、この決定木(条件分岐)を適用して最終的にどの集団に当てはまるのかをみて、当てはまった集団の数値を未知のデータ(顧客)の優良になる割合として予測するのである。この際の「条件」は、数理的に分岐によって優良率の濃淡が最も現れるものを採用している。実際に決定木が構築される流れを確認する。
まずは、図表2のように顧客全体に対してどの変数をどの閾値で分割すると最も優良率の濃淡が出るのかを探索して、結果として年齢の30歳を閾値とするのが最適だとして、分岐条件に採用される。
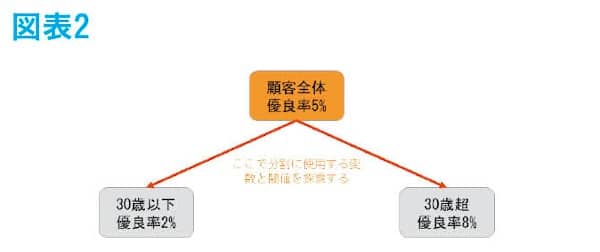
今度は顧客全体でなく「30歳以下」の集団のみに着目して、同様に優良率に最も濃淡ができる分岐を探索して、メールマガジンを購読しているかそうでないかで分岐するのが最適だとして、分岐条件に採用される。図表3のようにあくまで30歳以下の集団のみに適用される条件である。
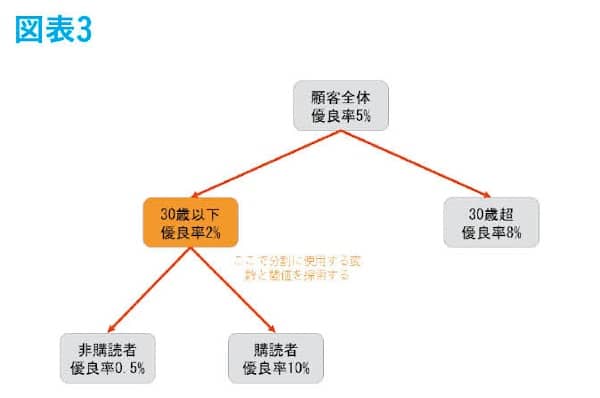
最後に30歳超の集団にも同様に分岐条件を探索すると、図表4のように、さらに年齢で分岐する条件が採用される。
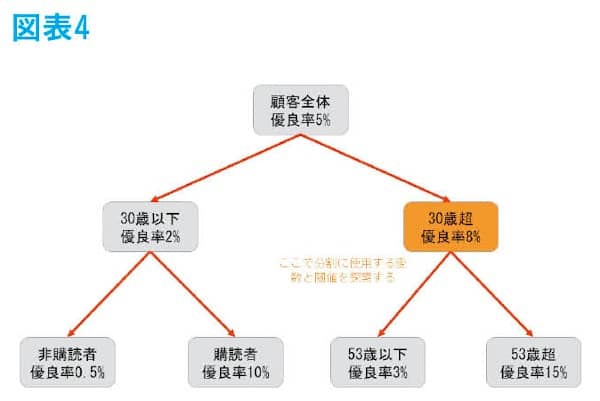
このようにしてできた集団の分割を決定木といい、AIとして社会の中で使用されている。ここで気づいた方もいるかもしれないが、この決定木はモデルが数式なしで可視化されているので、大変分かりやすいのが特徴の一つである。顧客や上司に対して説明がしやすいのである。また、よく耳にするディープラーニングや、決定木の発展系として知られている勾配ブースティング決定木と比較してもほとんど変わらない精度を出すこともしばしばある。ディープラーニングや勾配ブースティング決定木はブラックボックス型のモデルと言われ、予測結果に起因した要素が明確ではない。しかし、決定木では図のように予測値が付与された要因が明確である。したがって、他のモデルと比較して精度があまり変わらない問題で、字面の良さでディープラーニングじゃなきゃ絶対ダメという会社でなければ、決定木を使用する方が便利なことがある。
Python、Rでの実装例

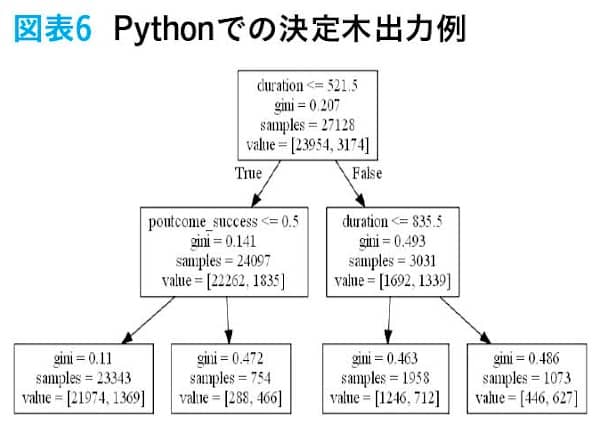
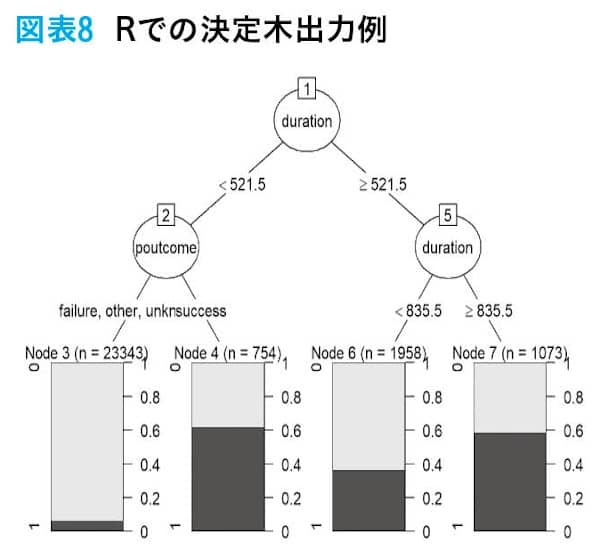
データ加工部分は省き、決定木モデル作成部分だけを掲載する。皆さんはAIと聞いて膨大なプログラムで記述されているものを想像した人がいるかもしれない。しかし、実際にはPythonやRで実装する場合、掲載したプログラムのように少ないコードで決定木モデルの学習ができる。ここではあくまで実装と決定木の出力のイメージを持っていただくことを目的とする。


過学習

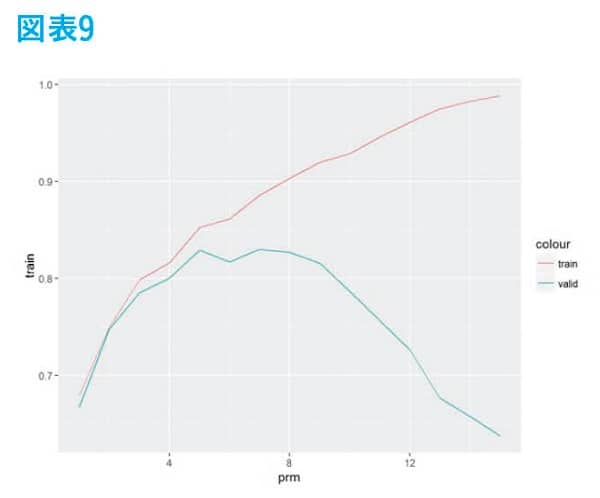
機械学習モデルでは、パラメータを変えたり、学習するデータによっては精度が異常に良くなったりするが、未知のデータに対する精度が下がるケースがある。掲載した例では縦軸が精度で値が高ければ良いものとし、横軸がパラメータの値とする。赤線が学習データでの精度で、パラメータを増やすと精度がどんどん上がっていくのが確認できる。しかし、緑色の線は未知のデータに対する精度で途中までは上がっていくが、あるところを過ぎると精度がどんどん下がっていく。このように学習データでは、精度が良いのに未知のデータに対する精度が悪い場合を「過学習」しているという。
したがって、モデル作成者はこの過学習を防ぎながら精度が高いパラメータを見つけたいわけである。しかし、本番運用で未知のデータが発生してから精度を確かめていては遅いので、蓄積された過去のデータから未知のデータでの予測精度を推し量る必要がある。その方法を次に解説する。
精度検証方法
蓄積された過去のデータを使って未知のデータでの精度を推し量る方法として下記の2つの方法が知られている。
Hold Out法
蓄積されたデータを任意の割合で「モデル構築用データ」と「モデル検証用データ」の2つに分割し、「モデル構築用データ」のみを使用してモデルを学習して「モデル検証用データ」で精度を確認する。このとき、「モデル検証用データ」はモデルからすると未知のデータであるので、実際の未知データに対する精度を推し量ることができる。
Cross Validation法
K分割交差検証法とも呼ばれ、HoldOut法の欠点を補った手法である。与えられた答えの分かっているデータをK個に分割し、そのうち1つを「モデル検証データ」にし、残りのK-1個を「モデル構築データ」とする。これによりモデルをK回構築することで、未知データへの予測精度を推し量る。

予測値の使い方
過学習していないモデルができたとして、次々回の第4回「評価指標を踏まえた運用の仕方」にて、実際に運用を踏まえた予測値の使い方を確認する。

- 寄稿
- Kaggle Master
佐野 遼太郎 氏Kaggle Masterの称号を持つ。2015年4月よりコンサルタントとして金融機関を中心としたデータ分析・モデル構築業務に従事。2018年2月にKaggler枠でディー・エヌ・エーに入社、現在はMobility Technologiesに出向中。また、2016年から社外データ分析講座講師として300人を超えるデータ分析技術者の人材育成に関わっている













