【連載】XVAの基礎と実践①　XVAの初歩～ CVA、FVAからMVA、KVAまで

1. XVAとはなにか？評価調整の背景について
2. 評価調整の種類と計算
   (１)CVA
   (２)FVA
   (３)COLVA
   (４)MVA
   (５)KVA
3. まとめ

XVAとはなにか？評価調整の背景について

2007年に始まった金融危機以降、デリバティブ取引の時価評価やリスク計測においては、カウンターパーティのデフォルトリスクの評価調整としてのCVA（Credit Value Adjustment）、ファンディングコスト／ベネフィットの評価調整としてのFVA（Funding Value Adjustment）の勘案が急速に広がった。
CVAは引当金（将来発生する可能性が高い費用や損失に対して、合理的に見積もられた金額で決算書にも記載される）に相当する重要な数字として位置づけられている。CVAはCDS（Credit Default Swap）などの市場価格と整合するように決められたデフォルト確率を用いて算出され、時価評価の一部をなすに至っている。市場変動の影響を受けて金額も日々変わるのでCVAデスクを設けるといった組織的な対応をする金融機関も多く、CVA額を管理できていないと逆選択により低採算な取引が集中するリスクがある（例えばデフォルトリスクの高いカウンターパーティの提示価格が、デフォルトリスクの低いカウンターパーティの提示価格と比べて魅力的に見えてしまうため）。
2021年に適用開始された「時価の算定に関する会計基準」において、時価とは「算定日において市場参加者間で秩序ある取引が行われると想定した場合の、当該取引における資産の売却によって受け取る価格又は負債の移転のために支払う価格をいう」と定められた。このタイミングに合わせて、従来はCVAなどを導入していなかった金融機関も導入を開始するに至った。
カウンターパーティリスクが意識されたことで担保授受の契約（例えばISDA（International Swaps and Derivatives Association）が定めるマスター契約に付随するCSA（Credit Support Annex））に対する注目度が拡大。担保の種類には変動証拠金（デフォルト時のポートフォリオ価値に対する担保金額、以下VM）や当初証拠金（デフォルト時から清算までの間におけるポートフォリオ価値の変化に対する担保金額、以下IM）があるが、まずはVMの有無をFVAとして反映する金融機関が急増した。その後は担保物の違いやVMに付利される金利の違いなどもCOLVA（Collateral Value Adjustment）として評価調整する金融機関も現れた（FVAやCOLVAに関しては一律な定義が確立されていないがここでは一例を述べている）。
さらには証拠金規制の拡大に伴ってIMを授受する金融機関が増え、評価調整としてのMVA（Margin Value Adjustment）への注目も高まっている。
バーゼル規制（国際的に活動する銀行に適用される最低所要自己資本に関して、バーゼル銀行監督委員会が国際統一基準として公表している）上の所要自己資本に関しても、規制の見直しに伴い、規制資本の調達コストに関する評価調整としてのKVA（Capital Value Adjustment）が注目を集めつつある。
以上で説明した様々な評価調整はXVAと総称されるが、より具体的なイメージをもってもらうために計算例を以下では説明する（XVAの定義は市場慣行として一律に定まっているわけではないが、著者が考える代表的な設定を紹介する）。

評価調整の種類と計算

分かりやすく説明するため極めて単純化された世界を例にとって説明する。ある仮想的な金融機関があるカウンターパーティとの間に保有するデリバティブポートフォリオの評価調整前の価値が10百万円（正だから受け取り側）とし、将来のある一定期間（以下、当該期間）における信用リスクなどを加味するとどのような評価調整が必要かを説明する。最終的にはこのような期間毎の各種評価調整の和（専門的になるのでここでは取り上げないが、時間に関する積分として定式化される）をとってポートフォリオの最終満期までの評価調整が得られる。

1. リスクフリーレートをr=0%、従って将来価値を現時点に割り引くためのディスカウントファクターをDF=1とする（実際とは異なるが以後の計算の数字を見やすくするためにこのように設定）。
2. 当該金融機関はVM=9.5百万円を現金で受け取っており、金利r_VM=0.01%を支払うとする（当該期間内に担保授受が複数回行われるとVMも変動するがここでは一定とする、言い換えるとそう仮定できる程度に当該期間を短くとっておく）。
3. IMに関しては受けと払いの両方が発生し、当該期間にIM_rec=1百万円を受け取って金利r_IMrec=0.01%を支払うと同時に、IM_pay=0.5百万円を支払って金利r_IMpay=0.01%を受け取るとする。
4. 当該金融機関の当該期間のファンディングスプレッド（リスクフリーレートへの上乗せ金利）をSP=0.3%とする。
5. カウンターパーティの当該期間のデフォルト確率をPD=10%、デフォルト時の非回収率をLGD=60%（デフォルトしてから回収終結までに回収できない割合）とする。ここで「確率」には実確率（過去データなどから統計的に決定される確率）とリスク中立確率（流動性の高い商品の市場価格と整合するように決められる確率）の2種類があるが、現在ではリスク中立確率を用いるのが市場慣行として定着しつつある。

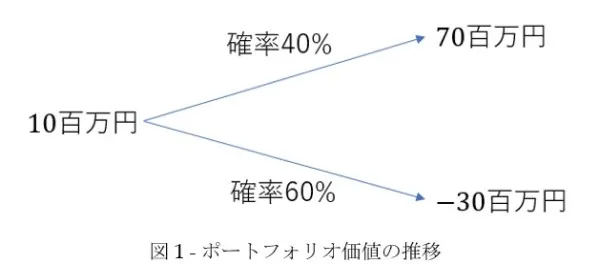
実際の計算では金利や為替など多くの市場変数を確率過程として数理モデルを構築し、乱数発生により将来の動きをシミュレーションすることで将来のポートフォリオ価値の確率分布が決まる。分かりやすく計算の雰囲気を伝えるために当該期間のポートフォリオ価値Vが上昇か下落か2つのパターンに限った確率分布（ここでもリスク中立確率）を考える。即ち、確率q=40%で上昇してV^u=70百万円になり、確率1-q=60%で下落してV^d=-30百万円になるとする。VMやIMも本来は確率分布を与えてシミュレーションされるものだが、本記事では定数として扱う。

(１)CVA

カウンターパーティが当該期間にデフォルトしたとき、担保でカバーされない損失金額（以下、エクスポージャー）は
E=V–VM–IM_rec
である。但しE≦0の場合は、当該金融機関の支払いサイドに該当するためカウンターパーティのデフォルトに伴う追加損失は発生しないので、正のエクスポージャーに関心がある。ポートフォリオ価値Vが上昇した場合は、
E^u=V^u–VM–IM_rec=70-9.5-1=59.5（百万円）
が正なので損失となり、下落した場合は、
E^d=V^d–VM–IM_rec=-30-9.5-1=-40.5（百万円）
が負なので損失額は0である。よって損失額の期待値は
EE=E^u×q+0×(1-q)=59.5×0.4=23.8（百万円）
となる（EEはExpected Exposureの略）。
当該期間のCVAは
CVA=-DF×LGD×EE×PD=-1×0.6×23.8×0.1=-1.428（百万円）
として計算される。
ここではカウンターパーティのデフォルトを考えたが、当該金融機関がデフォルトすることで、支払いを免除されるメリットを勘案するためのDVA（Debit Value Adjustment）と呼ばれる評価調整も存在する。但し、以下で述べるファンディングベネフィットに対する評価調整と概念上重複することが一般に指摘されているので注意を要する。

(２)FVA

ファンディングが必要な金額Fは
F=V–VM+IM_pay
で与えられる。
ポートフォリオ価値Vが上昇した場合は、
F^u=V^u–VM+IM_pay=70-9.5+0.5=61（百万円）
になり62百万円の調達が必要でファンディングコストがかかる（含み益はあるがすぐに受け取れない）。
ポートフォリオ価値Vが下落した場合は、
F^d=V^d–VM+IM_pay=-30-9.5+0.5=-39（百万円）
になり38百万円の運用が可能でファンディングベネフィットが出る（含み損はあるがすぐに払わなくてよい）。
ファンディング額の期待値EFは、
EF=F^u×q+F^d×(1-q)=61×0.4-39×0.6=24.4-23.4=1（百万円）
となる。
当該期間のFVAは
FVA=-DF×SP×EF=-1×0.003×1=-0.003（百万円）
として計算される。

(３)COLVA

当該期間のCOLVAは
COLVA=-DF×VM×(r_VM–r)=-1×9.5×0.0001=-0.00095（百万円）
として計算される。担保に付利される金利とリスクフリーレートの差額を調整するための働きをする。

(４)MVA

当該期間のMVAは
MVA=DF×{(r_IMpay–r)×IM_pay–r_IMrec×IM_rec}=1×(0.0001×0.5-0.0001×1)=-0.00005（百万円）
として計算される。IMの支払いに関しては、リスクフリーレートよりも大きい金利が付けば利益として計上される。IMの受け取りに関しては倒産隔離のため信託保管が義務付けられるので支払い金利そのものが損失として計上される。
IMをシミュレーションで計算する場合はその期待値を見積もることになるが、代表的な計算モデルであるISDA SIMMの場合、デリバティブの市場変数（金利や為替など）に関する感応度（グリークス）のシミュレーションが必要となるので、高い計算コストと技術を要する。

(５)KVA

所要自己資本をK=10百万円とし、その調達には金利r_K=5%相当分を要するものとすると、当該期間のKVAは
KVA=-DF×r_K×K=-1×0.05×10=-0.5（百万円）
として計算される。
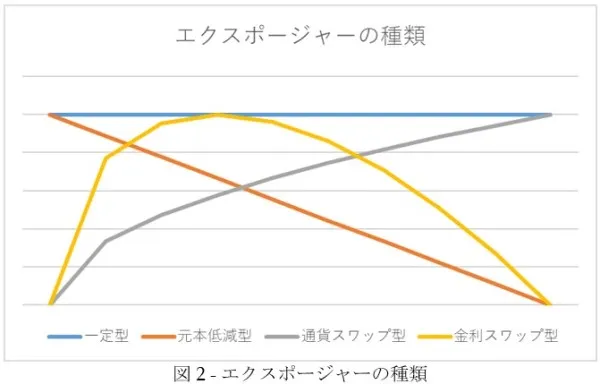
所要自己資本の（シミュレーションなどによる）見積もり額を将来の期間毎に変えて足し合わせることで、将来の（正の）エクスポージャーに整合的なコスト管理・採算管理ができるのがKVAのメリットである。図のようにエクスポージャー推移には商品性に応じた複数のパターンがあり、算定日の所要資本を勘案するだけでは採算判定を誤ることにつながりかねない。例えば、ローンと類似の性質を有する元本低減型の商品は契約当初から時間が経てばエクスポージャーが減衰するのでKVAを考えないと過度に資本コストを見積もることにつながる。その一方で、通貨スワップのように満期に異なる通貨の元本交換が発生する商品は契約当初から時間が経てばエクスポージャーが膨らむ傾向にあるので、KVAを考えないと過小に資本コストを見積もることにつながる。
また、証拠金規制開始前のCSA取引を信用力の高い中央清算期間にクリアリングすれば、所要資本が削減されてKVAも減少する傾向にあるが、IMが発生することに伴いMVAでデメリットが出る傾向にある。このようにあるXVAにメリットが出れば、別のXVAでデメリットが出る可能性があるので、関係性には注意を要する。

まとめ

デリバティブビジネスにおいて意識すべきXVAの種類は年々増えており、計算機性能や機械学習などの技術的発展に伴い、従来は考慮できなかったようなコスト／ベネフィットの新たな反映が今後も進むと考えられる。逆選択リスクを回避しつつ金融市場の流動性を高めて利便性を高めていくことが期待される。

寄稿

株式会社三菱UFJ銀行
融資企画部 CPM企画Gr 上席調査役
中山 季之 氏

2000年に東京三菱銀行（現三菱UFJ銀行）に入行。デリバティブの時価評価、リスク分析やトレーディングに従事する中で数理モデルの研究開発を継続してきた。現在は信用リスク管理業務に従事して規制CVAやカウンターパーティクレジットリスク計測などを担当。東京大学大学院 数理科学研究科博士課程修了（数理科学博士）。

▼連載記事一覧 【連載】XVAの基礎と実践