最新のオペレーショナルリスク規制とオペリスク所要自己資本

オペレーショナルリスク（オペリスク）とは

オペレーショナルリスクとは

オペレーショナルリスクとは、金融機関の業務の過程、役職員の活動、もしくはシステムが不適切であること、または外生的な事象により損失を被るリスク（規制自己資本比率の算定に含まれる分）および、金融機関自らがオペレーショナルリスクとして定めたリスク（規制自己資本比率の算定に含まれない分）をいう。

– 日本銀行 金融機構局 金融高度化センター
オペレーショナルリスク管理の現状と高度化への課題

オペレーショナルリスクの要因は、以下に例示したように様々あるが、これらの管理の不備は、経営破綻に追い込まれるなど経営に甚大な被害を与えるため、万が一に備えて十分な準備をしておく必要がある。

• 規程や手続きの不備などの内部体制の不備
• 事務ミス、不十分なチェックなどの人的要因
• 機器の故障やバグなどのシステム要因
• 自然災害や外部犯罪などの外生的要因

標準的手法（SMA）の改定

先進的計測手法（AMA）の除外。2016年3月4日にバーゼル銀行監督委員会（BCBS）から公表された、オペレーショナルリスクに係る資本枠組みの見直しに関する第二次市中協議案は、2014年10月の第一次案での問題意識を引き継ぎつつ、現行の規制を抜本的に簡素化する内容だ。

今次案に見られる標準的手法（SMA）改定は、一定の損益に掛目を適用してオペリスク所要自己資本とする考え方を継続しつつ、対象とする損益の構成や掛目の扱いを工夫することで、同資本のリスク感応度を上げることがねらいである。

わが国では国際統一基準行が対象となると思われる改定のポイントを、主要3指標の算定プロセスを中心に鳥瞰する。

SMA ＝ Standardized Measurement Approach、標準的手法

指標①：粗利益に代わる新指標

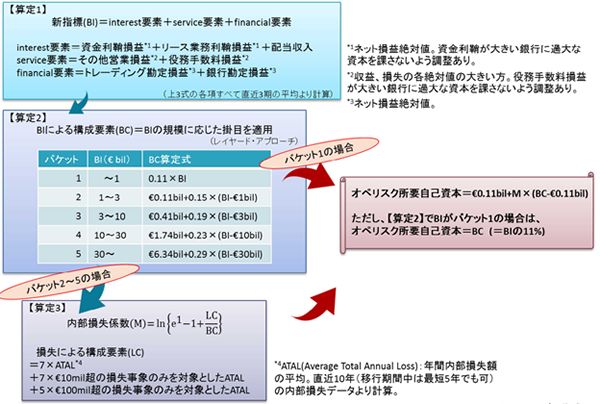
まず現行の粗利益に代わる新指標（BI：Business Indicator）の算定。interest、service、financialの3要素の和と表すことが可能だ。

interest要素は資金利鞘のネット損益絶対値が中心だが、リース業務や配当収入が含まれるほか、資金利鞘が大きい銀行に過大な資本を課さないよう調整（理屈上、利幅に3.5％のキャップ）がされる。

service要素は、その他営業損益と役務手数料損益（いずれも収益、損失の各絶対値の大きい方）の和だが、役務手数料損益が大きい銀行に過大な資本を課さないよう調整（同損益が調整前のBIの50％を超える場合、超えた部分は10分の1として調整しBIを計算）が加えられる。

financial要素はトレーディング勘定と銀行勘定のネット損益絶対値の和である。BIの算定に直近3期の平均を用いる点は、現行の粗利益の扱いと同様だ。

指標②：BIによる構成要素

指標のその2は、BIによる構成要素（BC：BI Component）だ。

所要自己資本計算上の掛目の構成要素をなすBCは、BIの規模別の5バケットに応じた5つの掛目（11％を最小とし、BIの規模つまり銀行の規模が大きくなるほど増加、最大29％）を適用して算定される。

BI規模の変化につれ隣り合うバケットで異なる掛目が適用されることでBCが非連続的に変化する「クリフ効果」を回避するために、レイヤード・アプローチ（BIが1段上のバケットになった場合に元のバケットからの超過金額に対してのみ、より高い掛目を適用する手法。わが国所得税の超過累進税率方式と同様）が採用されている。

ここでBI規模がバケット1の比較的小規模な銀行は、所要自己資本の計算が完了する。つまり、BIの11％がオペリスク所要自己資本となる。

指標③：内部損失係数

一方、BI規模がバケット2～5の銀行には、各行の内部損失実績を反映させ所要自己資本のリスク感応度を高めるプロセスが加わる。

このプロセスで算定される第3の指標は内部損失係数（M）だ。（協議案原文ではInternal Loss Multiplier）

Mの算定には損失による構成要素（LC：Loss Component）が必要。LCの計算には年間内部損失額の平均（ATAL：Average Total Annual Loss）（直近10年、ただし改定への移行期間中は最短5年も可）を利用する。

改定案のLCは、過去に発生した甚大な損失事象（分布のテール部分に相当）を所要自己資本の計算に適切に反映すべく、損失規模ごとに掛目を適用したATAL（ATALの7倍、€10百万超の損失事象のみを対象としたATALの7倍、€100百万超の損失事象のみを対象としたATALの5倍）の和となっている。

そして、MはBCおよびLC（LC/BC）をパラメータとした対数関数の形で定義されている（上図参照）。

以上を経て、BC算定時にバケット2～5の銀行のオペリスク所要自己資本は、BCに掛目Mを適用することで計算される。この掛目の適用においても、バケット1から2に移行する銀行のクリフ効果を避けるためのレイヤード・アプローチが見られる（バケット1に相当する€110百万を超える金額のみに掛目を適用）。

LC、所要自己資本、BCの大小ごとのオペリスクエクスポージャー

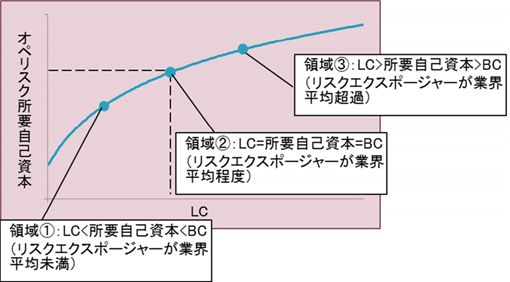
ここで、BC一定下の銀行のLC、所要自己資本RC、BCの大小ごとのオペリスクエクスポージャーをイメージすると、以下のように理解できる。

• 領域①（LC＜RC＜BC）の銀行：業界平均未満
• 領域②（LC＝RC＝BC）の銀行：業界平均程度
• 領域③（LC＞RC＞BC）の銀行：業界平均超過

なお、この場合、所要自己資本はLCの対数関数となり、LC増加（内部損失実績増加）はRCを増加させるが、その増加ペースは漸減する。

まとめ

最後に、今次SMA改定に伴い、AMAは、金融機関ごとの取扱データや計算手法の違いが大きく計算結果の相互比較が困難とされ、オペリスク規制の枠組みから除外されることとなった。AMAに知恵を絞ってきた金融機関はリスク管理高度化の再考を迫られるであろう。

本市中協議案のパブコメ（～6月3日）や最終的なカリブレーションの参考のための定量的影響度調査（QIS）を経て、年内にSMA改定やAMA除外の詳細スケジュールが明らかになる。

転載元：IN-BRIEF INSIGHTS （株式会社ファルチザンウェブサイト）